PITAGORAS DE SAMOS
Fue un filósofo y matemático griego considerado el primer matemático puro. Contribuyó de manera significativa en el avance de la matemática helénica, la geometría y la aritmética, derivadas particularmente de las relaciones numéricas, y aplicadas por ejemplo a la teoría de pesos y medidas, a la teoría de la música o a la astronomía. Es el fundador de la Hermandad Pitagórica, una sociedad que, si bien era de naturaleza predominantemente religiosa, se interesaba también en medicina, cosmología, filosofía, ética y política, entre otras disciplinas. El pitagorismo formuló principios que influyeron tanto en Platón como enAristóteles y, de manera más general, en el posterior desarrollo de la matemática y en la filosofía racional en Occidente.
No se conserva ningún escrito original de Pitágoras. Sus discípulos los pitagóricos invariablemente justificaban sus doctrinas citando la autoridad del maestro de forma indiscriminada, por lo que resulta difícil distinguir entre los hallazgos de Pitágoras y los de sus seguidores. Se le atribuye a Pitágoras la teoría de la significación funcional de los números en el mundo objetivo y en la música; otros descubrimientos, como lainconmensurabilidad del lado y la diagonal del cuadrado o el teorema de Pitágoras para los triángulos rectángulos, fueron probablemente desarrollados por la escuela pitagórica.
BIOGRAFÍA
Parece seguro que Pitágoras fue hijo de Mnesarco y que la primera parte de su vida la pasó en Samos, la isla que probablemente abandonó unos años antes de la ejecución de su tirano Polícrates, en el 522 a.C. Es posible que viajara entonces a Mileto, para visitar luego Fenicia y Egipto; en este último país, cuna del conocimiento esotérico, se le atribuye haber estudiado los misterios, así como geometría y astronomía.
Algunas fuentes dicen que Pitágoras marchó después a Babilonia con Cambises, para aprender allí los conocimientos aritméticos y musicales de los sacerdotes. Se habla también de viajes a Delos, Creta y Grecia antes de establecer, por fin, su famosa escuela en Crotona, donde gozó de considerable popularidad y poder.
La comunidad liderada por Pitágoras acabó, plausiblemente, por convertirse en una fuerza política aristocratizante que despertó la hostilidad del partido demócrata, de lo que derivó una revuelta que obligó a Pitágoras a pasar los últimos años de su vida en Metaponto.
La comunidad pitagórica estuvo seguramente rodeada de misterio; parece que los discípulos debían esperar varios años antes de ser presentados al maestro y guardar siempre estricto secreto acerca de las enseñanzas recibidas. Las mujeres podían formar parte de la cofradía; la más famosa de sus adheridas fue Teano, esposa quizá del propio Pitágoras y madre de una hija y de dos hijos del filósofo.
El pitagorismo fue un estilo de vida, inspirado en un ideal ascético y basado en la comunidad de bienes, cuyo principal objetivo era la purificación ritual de sus miembros a través del cultivo de un saber en el que la música y las matemáticas desempeñaban un papel importante. El camino de ese saber era la filosofía, término que, según la tradición, Pitágoras fue el primero en emplear en su sentido literal de «amor a la sabiduría».
También se atribuye a Pitágoras haber transformado las matemáticas en una enseñanza liberal mediante la formulación abstracta de sus resultados, con independencia del contexto material en que ya eran conocidos algunos de ellos; éste es, en especial, el caso del famoso teorema que lleva su nombre y que establece la relación entre los lados de un triángulo rectángulo, una relación de cuyo uso práctico existen testimonios procedentes de otras civilizaciones anteriores a la griega.
La voluntad unitaria de la doctrina pitagórica quedaba plasmada en la relación que establecía entre el orden cósmico y el moral; para los pitagóricos, el hombre era también un verdadero microcosmos en el que el alma aparecía como la armonía del cuerpo. En este sentido, entendían que la medicina tenía la función de restablecer la armonía del individuo cuando ésta se viera perturbada, y, siendo la música instrumento por excelencia para la purificación del alma, la consideraban, por lo mismo, como una medicina para el cuerpo. La santidad predicada por Pitágoras implicaba toda una serie de normas higiénicas basadas en tabúes como la prohibición de consumir animales, que parece haber estado directamente relacionada con la creencia en la transmigración de las almas; se dice que el propio Pitágoras declaró ser hijo de Hermes, y que sus discípulos lo consideraban una encarnación de Apolo.
LA HERMANDAD PITAGÓRICA
Pitágoras fundó una escuela filosófica y religiosa en Crotona, al sur de Italia, que tuvo numerosos seguidores. Se llamaban a sí mismos matemáticos, vivían en el seno de esta sociedad de forma permanente, no tenía posesiones personales y eran vegetarianos. Hasta 300 seguidores llegaron a conformar este grupo selecto, que oía las enseñanzas de Pitágoras directamente y debía observar estrictas reglas de conducta. Sus máximas pueden sintetizarse como:
- que en su nivel más profundo, la realidad es de naturaleza matemática;
- que la filosofía puede usarse para la purificación espiritual;
- que el alma puede elevarse para unirse con lo divino;
- que ciertos símbolos son de naturaleza mística;
- que todos los miembros de la hermandad deben guardar absoluta lealtad y secretismo.
En la Hermandad Pitagórica eran aceptados tanto hombres como mujeres. Aquellos que no pertenecían al núcleo duro del grupo eran llamados acusmáticos. Éstos vivían en sus propias casas, se les permitía tener posesiones personales y no se les imponía el vegetarianismo; sólo asistían como oyentes durante el día. Según Krische, las mujeres pertenecían a este grupo; no obstante, muchas pitagóricas fueron después reconocidas filósofas y matemáticas.
La escuela practicaba el secretismo y la vida comunal de manera muy estricta, y sus miembros solían atribuir todos sus descubrimientos a su fundador. De darles crédito, el alcance y la cantidad de trabajo de Pitágoras tendría una extensión inverosímil; aunado a esto, no se conserva ningún escrito de Pitágoras propiamente, por lo que la distinción entre sus trabajos y los de sus seguidores es de difícil demarcación. Las contribuciones de los pitagóricos y su enorme influencia fueron determinantes para el desarrollo las matemáticas, la astronomía y la medicina, entre otras ciencias naturales, y es razonable dar crédito a Pitágoras por muchos de sus hallazgos.
LAS MATEMÁTICAS EN PITAGORAS
La ciencia matemática practicada por Pitágoras y los matematikoi difiere del tratamiento de esta ciencia que se lleva a cabo en universidades o instituciones modernas. Los pitagóricos no estaban interesados en «formular o resolver problemas matemáticos», ni existían para ellos problemas abiertos en el sentido tradicional del término. El interés de Pitágoras era el de «los principios» de la matemática, «el concepto de número», el concepto de triángulo y la idea abstracta de prueba.
Pitágoras reconocía en los números propiedades tales como personalidad, masculinos y femeninos, perfectos o imperfectos, bellos y feos. El número diez era especialmente valorado, por ser la suma de los primeros cuatro enteros [1 + 2 + 3 + 4 = 10], los cuales se pueden disponer en forma de triángulo perfecto: la «tetraktys». Para los pitagóricos, «las cosas son números», y observaban esta relación en el cosmos, la astronomía o la música.
Entre los descubrimientos matemáticos que se atribuyen a la escuela de Pitágoras se encuentran:
TEOREMA DE PITAGORAS:
El teorema de Pitágoras lleva este nombre porque su descubrimiento recae sobre la escuela pitagórica. Anteriormente, en Mesopotamia y el Antiguo Egipto se conocían ternas de valores que se correspondían con los lados de un triángulo rectángulo, y se utilizaban para resolver problemas referentes a los citados triángulos, tal como se indica en algunas tablillas y papiros. Sin embargo, no ha perdurado ningún documento que exponga teóricamente su relación. La pirámide de Kefrén, datada en el siglo XXVI a. C., fue la primera gran pirámide que se construyó basándose en el llamado triángulo sagrado egipcio, de proporciones 3-4-5.
Si un triángulo rectángulo tiene catetos de longitudes
De la ecuación se deducen fácilmente 3 corolarios de aplicación práctica:
Pitágoras ( c²=a²+b² ) – Fórmulas prácticas
Aca Una Explicacion:
SOLIDOS PLATONICOS:
TABLA COMPARATIVA
| Sólidos Platónicos | Tetraedro | Hexaedro, Cubo | Octaedro | Dodecaedro | Icosaedro |
|---|---|---|---|---|---|
 |  |  |  |  | |
| Animación |  |  |  |  |  |
| Desarrollo |  | 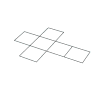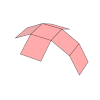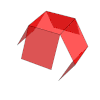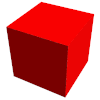 | 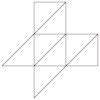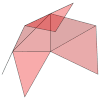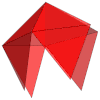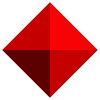 |  |  |
| Número de caras | 4 | 6 | 8 | 12 | 20 |
| Polígonos que forman
las caras
| Triángulos Equiláteros | Cuadrados | Triángulos Equiláteros | Pentágonos Regulares | Triángulos Equiláteros |
| Número de aristas | 6 | 12 | 12 | 30 | 30 |
| Número de vértices | 4 | 8 | 6 | 20 | 12 |
| Caras concurrentes
en cada vértice
| 3 | 3 | 4 | 3 | 5 |
| Vértices contenidos
en cada cara
| 3 | 4 | 3 | 5 | 3 |
| Grupo de simetría | Tetraédrico (Td) | Hexaédrico (Hh) | Octaédrico (Oh) | Icosaédrico (Lh) | Icosaédrico (Lh) |
| Poliedro conjugado | Tetraedro (autoconjugado) | Octaedro | Hexaedro, Cubo | Icosaedro | Dodecaedro |
| Símbolo de Schläfli | {3,3} | {4,3} | {3,4} | {5,3} | {3,5} |
| Símbolo de Wythoff | 3 | 2 3 | 3 | 2 4 | 4 | 2 3 | 3 | 2 5 | 5 | 2 3 |
| Ángulo diedro | 70.53° = arccos(1/3) | 90° | 109.47° = arccos(-1/3) | 116.56° | 138.189685° |
| Radio externo |  |  |  |  |  |
 |  |  |  |  |  |
| Radio interno |  |  |  |  |  |
 |  |  |  |  |  |
- Ángulos interiores de un triángulo. Encontraron que la suma de los ángulos interiores de un triángulo es igual a dos rectos, así como la generalización de este resultado a polígonos de n - lados.
- La irracionalidad de la raíz cuadrada de 2. Los pitagóricos descubrieron que la diagonal de un cuadrado de lado 1 no puede expresarse como un cocientede números enteros. Este evento marca el descubrimiento de los números irracionales, si bien a la época, sólo podía entenderse en términos deinconmensurabilidad de magnitudes [números] enteras, o «proporciones geométricas». Un método de aproximación (aproximación diofántica) posiblememente desarrollado por Arquitas, utiliza el algoritmo de Euclides, y está presente en Los Elementos.
- El descubrimiento de los Números perfectos y los Números amigos. Jámblico atribuye a Pitágoras el haber descubierto el par de números amigos (220, 284).
- Medias. Los pitagóricos examinaron exhaustivamente las razones y proporciones entre los números enteros; la media aritmética, la media geométrica y la media armónica y las relaciones entre ellas.
- El descubrimiento de los Números poligonales. Un número es «poligonal» (triangular, cuadrangular, pentagonal, hexagonal, etc.) si tal número de puntos se pueden acomodar formando el polígono correspondiente (ver figura).
- Tetraktys. Se atribuye a Pitágoras el haber ideado la Tetraktys, la figura triangular compuesta por diez puntos ordenados en cuatro filas. Fue un símbolo de especial importancia para los pitagóricos, que solían juramentar en su nombre.

PITAGORAS EN LA ASTRONOMÍA
Pitágoras enseñaba que la Tierra estaba situada en el centro del universo, y que la órbita de la Luna estaba inclinada hacia el ecuador de la Tierra; fue de los primeros en revelar que el Lucero del alba era el mismo planeta que el Lucero de la tarde, Venus. Sin embargo, según Teofrasto, fue Parménides quien descubrió la esfericidad de la Tierra, así como la identidad del Lucero del alba; la autoría de Pitágoras parece provenir de un poema dedicado a él, así como de la tradición que sitúa a Parménides como alumno de Pitágoras.
Filolao afirmaba que la Tierra se movía, pero no sobre su propio eje, sino alrededor del fuego central, concepto que no equivalía al Sol, sino que para él era una fuerza situada en el centro del mundo. El descubrimiento de la rotación de la Tierra alrededor de su eje se atribuye al pitagórico Hicetas de Siracusa, idea que también enseñaban Ecfanto de Siracusa y Heráclides Póntico. La teoría de un movimiento combinado de la Tierra alrededor de su propio eje y también alrededor del Sol, en cambio, no fue obra de los pitagóricos sino que fue afirmada por primera vez por Aristarco de Samos, astrónomo aristotélico.
Planteo tres Paradigmas:
1.- Los planetas, el Sol, la luna y las estrellas se mueven en órbitas circulares perfectas.
2.- La velocidad de los astros es perfectamente uniforme.
3.- La Tierra se encuentra en el centro exacto de los cuerpos celestes.
PITAGORAS EN LA MÚSICA:
Se le adjudica a Pitágoras el descubrimiento de las leyes de los intervalos musicales regulares, es decir, las relaciones aritméticas de la escala musical. Diógenes Laercio le atribuye la invención del monocordio, un instrumento musical de una sola cuerda. Ilustra la ley según la cual la altura del sonido es inversamente proporcional a la longitud de la cuerda. Los principios de la música fueron sin duda tan importantes para el sistema pitagórico como los principios matemáticos mismos, o las nociones sobre números. La expresión de la Naturaleza en términos matemáticos -como las proporciones y las razones- es una idea clave dentro de la filosofía desarrollada por los pitagóricos. Estos filósofos notaron que todos los modos de la armonía musical y las relaciones que la componen se resuelven con números proporcionales.

La afinación pitagórica es una gama musical construida sobre intervalos de quintas perfectas de razón 3/2. Las frecuencias pitagóricas de la nota Do son las siguientes: 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048...
Para los pitagóricos la música poseía además un valor ético y medicinal, Pitágoras hacía comenzar la educación por la música, por medio de ciertas melodías y ritmos, gracias a los cuales sanaba los rasgos de carácter y las pasiones de los hombres, atraía la armonía entre las facultades del alma. La idea del orden y de que las relaciones de armonía regulan incluso todo el universo, se encuentran presentes en todo el sistema pitagórico. La armonía del cuerpo y la armonía del cosmos eran vistas por igual, dentro de un sistema unificador. Platón dirá que música y astronomía son ciencias hermanas. La música planetaria o armonía de las esferas.
Pitágoras habría establecido que las distancias entre las órbitas del Sol, de la Luna y de las estrellas fijas corresponden a las proporciones octava, quinta y cuarta, de la voz de los siete planetas de la esfera de las [estrellas] fijas y de la esfera encima nuestro que llamamos Anti-Tierra, hacía las nueve Musas. Los intervalos(espaciales) entre los cuerpos celestes se disponían de acuerdo con las leyes y relaciones de la armonía musical. Los cuerpos celestes en su movimiento no podían no ocasionar un cierto sonido o incluso notas, dependiendo de sus distancias y velocidades, determinadas por las leyes de los intervalos armónicos (musicales), las notas en conjunto formaban una escala musical regular o armoniosa; esta música no la podemos oír, ya sea porque siempre hemos estado acostumbrados a ella y no la podemos distinguir, o porque el sonido es tan potente que escapa a nuestras capacidades auditivas» (Aristóteles, Porfirio). Pitágoras tendía su oído y fijaba su intelecto sobre los acordes celestes del universo. Él solo, por lo que parece, escuchaba y comprendía la armonía y el unísono universales de las esferas [planetarias] y de los astros.

No hay comentarios:
Publicar un comentario